A.
Pengertian.
Critical Section
adalah bagian dari suatu proses yang akan melakukan akses dan manipulasi data. Ketika sebuah proses sedang
dijalankan dalam critical section nya, tidak ada proses lain
yang boleh dijalankan dalam critical section tersebut, karena akan
menyebabkan keadaan mutually exclusive.
Mutually exclusive yakni keadaan
terjadinya akses resources yang sama di saat
yang bersamaan. Mutually exclusive
memerlukan kondisi tertentu agar dapat terpenuhi.
Critical section biasanya
digunakan saat program multithreading, dimana program
tersebut terdiri dari banyak thread, akan
mengubah nilai dari variabel. Dalam hal
ini critical sectiondiperlukan
untuk melindungi variabel dari concurrent access (pengaksesan
program di saat yang bersamaan) yang dapat membuat nilai dari variabel tersebut menjadi tidak konsisten. Seperti yang telah kita ketahui bahwa
proses dapat bekerja sendiri (independent process) dan juga dapat bekerja bersama
proses-proses yang lain (cooperating process). Pada umumnya ketika proses saling bekerjasama (cooperating
process) maka proses-proses tersebut akan
saling berbagi data. Pada saat proses-proses berbagi data, ada kemungkinan
bahwa data yang dibagi secara bersama itu akan menjadi tidak
konsisten dikarenakan adanya kemungkinan
proses-proses tersebut melakukan akses
secara bersamaan yang menyebabkan data
tersebut berubah, hal ini dikenal dengan istilah Race
Condition.
Oleh
karena itu, dibutuhkan solusi yang tepat
untuk menghindari munculnya Race Condition.
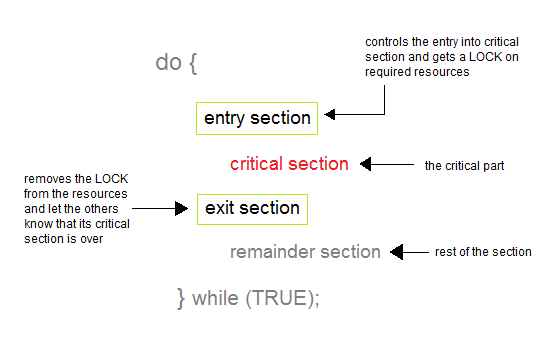
Solusi tersebut harus memenuhi ketiga syarat berikut :
01.) Mutual Exclusion.
Jika suatu proses sedang menjalankan critical
section-nya, maka proses-proses lain tidak dapat menjalankan critical section
mereka. Dengan kata lain, tidak ada dua proses
yang berada di critical section pada saat
yang bersamaan.
02.) Progress.
Jika tidak ada proses yang sedang menjalankan critical section-nya dan ada proses-proses lain
yang ingin masuk ke critical section, maka
hanya proses-proses yang yang sedang berada dalam entry
section saja yang dapat berkompetisi
untuk mengerjakan critical section.
03.) Bounded Waiting.
Jika seandainya ada proses yang sedang menjalankan critical section, maka proses
lain memiliki waktu
tunggu yang ada batasnya untuk menjalankan
critical section-nya, sehingga dapat
dipastikan bahwa proses tersebut dapat mengakses critical
section-nya (tidak mengalami starvation:
proses seolah-olah berhenti, menunggu request
akses ke critical
section diperbolehkan).
B.
Solusi
untuk Critical Section.
01.) Solusi Perangkat Lunak.
Solusi ini menggunakan algoritma-algoritma untuk mengatasi masalah critical section.
Berikut ini algoritma-algoritma yang
digunakan untuk mengatasi masalah critical section
:
a.) Algoritma I.
Algoritma I
memberikan giliran kepada setiap proses untuk memproses
critical section-nya secara bergantian.
Asumsi yang digunakan disini setiap proses secara bergantian
memasuki critical section-nya. Statement while(turn != 4)
akan memeriksa apakah pada saat itu proses 4
mendapatkan turn, jika tidak maka proses 4 akan busy waiting(lihat
kembali bahwa printah while diakhiri dengan
“;”). Jika ternyata pada saat itu merupakan giliran proses
4 maka proses
4 akan mengerjakan critical
section-nya. Sampai sini jelas terlihat bahwa mutex
terpenuhi! Proses yang tidak mendapatkan turn tidak akan dapat mengerjakan critical section-nya dan turn
hanya akan diberikan pada satu proses saja.

Setelah proses 4 selesai
mengerjakan critical section maka turn diberikan pada proses
lainnya (turn= j,
j merupakan proses selanjutnya yang dapat
mengerjakan critical section). Setelah turn-nya diberikan kepada proses lain, proses 4 akan mengerjakan remainder
section. Disini jelas terlihat bahwa syarat bounded waiting
jelas terpenuhi. Ingat asumsi yang digunakan
dalam algoritma ini adalah setiap proses
secara bergantian memasuki critical section-nya, jika pada saat itu proses 4 ternyata belum mau mengerjakan critical section-nya maka proses
ke-j tidak akan mendapatkan kesempatan untuk
mengerjakan critical section walau saat itu
sebenarnya proses ke-j akan memasuki critical section.
Artinya syarat progress tidak terpenuhi pada
algoritma ini.
b.) Algoritma II.
Masalah yang terjadi
pada algoritma
1 ialah ketika di entry section
terdapat sebuah proses yang ingin masuk ke critical
section, sementara di critical section
sendiri tidak ada proses yang sedang
berjalan, tetapi proses yang ada di entry section tadi tidak bisa masuk ke critical section. Hal ini terjadi karena giliran untuk memasuki critical
section adalah giliran proses yg lain
sementara proses tersebut masih berada di remainder section. Untuk mengatasi masalah ini
maka dapat diatasi dengan merubah variabel turn pada algoritma
pertama dengan array
Boolean flag.

Elemen
array diinisialisasi
false. Jika flag[i] true, nilai
tersebut menandakan bahwa Pi ready untuk
memasuki critical section. Pada algoritma ini, hal pertama yang dilakukan ialah mengeset proses Pi dengan nilai True, ini menandakan bahwa Pi ready untuk masuk ke critical
section. Kemudian, Pi memeriksa
apakah Pj tidak ready
untuk memasukui critical section.
Jika Pj ready, maka Pi
menunggu sampai Pj keluar dari critical section (flag[j] bernilai false).
Ketika keluar dari critcal
section, Pi harus merubah nilai flag[i] menjadi
false agar prores
lain dapat memasuki critical section.
ex :
Pada algoritma
ini, kriteria Mutual-exclusion terpenuhi,
tetapi tidak memenuhi kriteria progress.
Ilustrasinya seperti di bawah ini.
T0
: Po set flag
[0] = true
T1
: Po set flag
[1] = true
Dari ilustrasi diatas
terlihat bahwa algoritma ini memungkinkan
terjadinya nilai true untuk kedua proses, akibatnya tidak ada proses yang akan berhasil memasuki critical section. Jadi untuk algoritma 2
masih terdapat kelemahan, seperti yang
terjadi di atas.
c.) Algoritma III.
Idenya berasal
dari algoritma
1 dan 2. Algoritma 3 mengatasi kelemahan pada
algoritma
1 dan 2 sehingga progres yang
diperlukan untuk mengatasi critical section terpenuhi.

Algoritma III
ditemukan oleh G.L. Petterson pada tahun 1981 dan dikenal juga sebagai Algoritma Petterson. Petterson
menemukan cara yang sederhana untuk mengatur proses
agar memenuhi mutual exclusion. Algoritma ini adalah solusi untuk memecahkan
masalah critical section pada dua proses. Ide dari
algoritma ini adalah menggabungkan variabel yang di- sharing pada
Algoritma
I dan Algoritma II, yaitu variabel turn dan variabel flag.
Sama seperti pada Algoritma I dan II, variabel turn menunjukkan
giliran proses mana yang diperbolehkan
memasuki critical section dan variabel flag menunjukkan apakah suatu
proses membutuhkan akses ke critical section atau
tidak.
Awalnya flag untuk kedua proses diinisialisai bernilai false, yang artinya kedua proses
tersebut tidak membutuhkan akses ke critical section. Kemudian jika suatu proses ingin memasuki critical section, ia akan mengubah flag-nya menjadi true (memberikan
tanda bahwa ia butuh critical section) lalu proses tersebut
memberikan turn kepada lawannya. Jika lawannya
tidak menginginkan critical section (flag-nya false),
maka proses tersebut dapat menggunakan critical
section, dan setelah selesai menggunakan critical
section ia akan mengubah flag-nya
menjadi false. Tetapi apabila proses lawannya juga menginginkan critical section maka proses lawan-lah yang dapat memasuki critical section, dan proses
tersebut harus menunggu sampai proses lawan menyelesaikan critical
section dan mengubah flag-nya
menjadi false.

Misalkan ketika P0 membutuhkan critical
section, maka P0 akan mengubah flag[0] = true, lalu P0
mengubah turn= 1. Jika P1
mempunyai flag[1]
= false, (berapapun nilai turn) maka P0
yang dapat mengakses critical section.
Namun apabila P1 juga membutuhkan critical section, karena flag[1] = true dan turn=
1, maka P1
yang dapat memasuki critical section dan
P0 harus menunggu sampai P1 menyelesaikan critical
section dan mengubah flag[1] = false,
setelah itu barulah P0 dapat mengakses critical section.
d.) Algoritma Tukang Roti.
Algoritma
ini
didasarkan pada algoritma penjadwalan yang
biasanya digunakan oleh tukang roti, dimana urutan pelayanan
ditentukan dalam situasi yang sangat sibuk. Algoritma
ini dapat digunakan untuk memecahkan masalah critical
section untuk n buah proses, yang diilustrasikan dengan n buah pelanggan.
Ketika memasuki toko, setiap pelanggan
menerima sebuah nomor. Sayangnya, algoritma
tukang roti ini tidak dapat menjamin bahwa dua proses
(dua pelanggan) tidak akan menerima nomor yang sama. Dalam kasus di mana dua proses menerima nomor
yang sama, maka proses dengan nomor ID terkecil yang akan dilayani dahulu. Jadi, jika Pi dan Pj
menerima nomor yang sama dan i < j, maka Pi
dilayani dahulu. Karena setiap nama proses
adalah unik dan berurut,
maka algoritma ini dapat digunakan untuk
memecahkan masalah critical section untuk
n buah proses.
Struktur data
umum algoritma ini adalah
boolean choosing[n];
int number [n];
Awalnya, struktur data ini diinisialisasi
masing-masing ke false dan 0, dan menggunakan notasi
berikut :
» (a,
b) < (c, d) jika a < c atau jika a= c dan b < d
» max(a0,
…, an-1) adalah sebuah bilangan k, sedemikian sehingga k >= ai untuk setiap
i= 0, …, n – 1
Dengan demikian, diketahui
bahwa Algoritma I dan II terbukti tidak dapat memecahkan masalah critical section untuk dua
proses karena tidak memenuhi syarat progress
dan bounded waiting. Algoritma yang dapat menyelesaikan masalah critical section pada dua
proses adalah Algoritma III. Sedangkan
untuk masalah critical section pada n-buah proses
dapat diselesaikan dengan menggunakan Algoritma Tukang Roti.
02.) Solusi Perangkat Keras.
Solusi ini tergantung
pada beberapa instruksi mesin tertentu, misalnya dengan me-non-aktifkan interupsi, mengunci suatu variabel
tertentu atau menggunakan instruksi level mesin
seperti tes dan set.
Referensi.
- https://en.wikipedia.org/wiki/Critical_section
- http://pengertian-istilah.blogspot.com/2014/12/pengertian-critical-section.html
- http/mediekaputra.wordpress.com/2011/03/26/critical-section/
- http://www.infomugi.com/2013/07/penjelasan-solusi-critical-section.html
- http://ftp.gunadarma.ac.id/linux/docs/v06/Kuliah/SistemOperasi/BUKU/SistemOperasi-4.X-1/ch18s02.html
Tidak ada komentar:
Posting Komentar